|
Modelado y Simulación de Sistemas Dinámicos Reporte 3 |

|
Herramientas utilizadas
- Octave - Lenguaje de programación utilizado
- Gnuplot - Para creación de gráficas
Dado a que use Octave para hacer mi tarea, y además de que trate de no repetir generadores de números pseudoaleatorios con distribuciones que mis compañeros ya habían usado en su tarea, tome la función para generar números pseudoaleatorios con la Distribución Beta.
La función es llamada de la siguiente forma.
betarnd(alpha, beta)La cual nos regresa un número aleatorio de punto flotante entre 0 y 1.
Y cuya función de densidad esta dada por la siguiente forma.
¿Los números generados de acoplan a la distribución indicada?
Para saber si los números generados en verdad se acoplan a la distribución dada, lo que hice fue crear un pequeño programa en octave que genera una cantidad N de números aleatorios en la distribución beta, dándole como parámetros el valor de alfa = 2 y beta = 2.
Estos valores generados los iba ubicando en "canastas", para después graficar y saber si se parecía a la función.
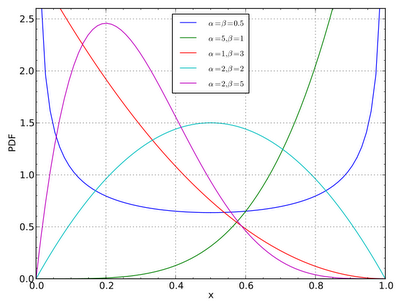
En un principio lidie un poco con la parte de cual función era la correcta, pero en la página de la Wikipedia vienen unas gráficas y sus respectivos valores de alfa y beta dados, y en primera instancia compare directamente con esa gráfica que es la siguiente.
Y que para los valores que yo di, debería de parecerse a la de la línea color aqua.
Mi programa fue el siguiente.
Y con los datos recabados desde el anterior grafique directo con gnuplot para obtener lo siguiente.
betadis(1000, 100)
betadis(10000, 100)
Hasta ese momento fue un suspiro ver que mientras más aumentaba la cantidad de repeticiones, que son la cantidad de números generados, para un total de 100 canastas, los puntos marcados se acercaban más a la gráfica de la función.
Luego hice algo diferente, gracias a la idea de Juan Carlos para graficar y comparar directamente con la gráfica de la función, que por cierto es la de Función de Densidad. Primero cree un archivo con 10mil números aleatorios con la distribución.
Para después con Gnuplot crear un histograma y ahí mismo colocar la función de densidad para la distribución beta.
El resultado en imagen fue el siguiente.
Y con la imagen anterior, llegué a la conclusión de que el generador de números pseudoaleatorios, si se acopla a la distribución beta.
¿Los números generados presentan características deseables de números aleatorios?
Ahora faltaba hacer alguna prueba para verificar que los números generados tienen la característica de números aleatorios.
Al final esta el enlace a la página donde se encuentran todos las pruebas que se consideran como excelentes para verificar esto, también en el PDF de Statistical Test Suite, ahi vienen explicados todos las pruebas, así como en la página de random.org.
Hice la prueba de frecuencia por bloques, que trata de verificar que la cantidad de ceros y unos por bloque de un arreglo total de números sea pareja.
Donde la cantidad de bloques N esta dado por n/m, donde n es el número de elementos, y m la cantidad de elementos por bloque.
Al correr esta prueba, obtuve que el generador paso por lo menos esta de las tantas pruebas que hay, y probé con esa cantidad en los parámetros, intente con más pero tardo mucho y cancele.
Y esto fue todo, pero por último menciono como dato, que en Gnuplot y Octave la función log, es tomada como logaritmo natural, y para el logaritmo base 10 la función es log10, cosa que casi me mete en problemas, pero en los tutoriales encontré esa información.
Recursos consultados
Tutorial Gnuplot
Tutorial Octave
Statistical Test Suite
Distribución Beta
Pruebas estadísticas




Bien; 5 y 5 con los castigos de retardo de -1.
ResponderEliminar